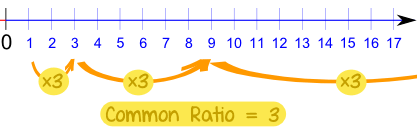
1. Patterns
- set of number or sequence.
- Repeated design or recurring sequence.
- An ordered set of numbers, shapes or other mathematical objects, arranged according to a rule.
Try to get the pattern of this picture
Short video about Math Patterns...
Sequence
A Sequence is a succession of numbers in a specific order.Each number in a sequence is called terms. The terms are formed according to some fixed rule or property. They are arranged as the first term, the second term, the third term and so on. A sequence with a definite number of term is a finite sequence.
Examples:
{1, 2, 3, 4, ...} is a very simple sequence (and it is an infinite sequence)
{20, 25, 30, 35, ...} is also an infinite sequence
{1, 3, 5, 7} is the sequence of the first 4 odd numbers (and is a finite sequence)
{4, 3, 2, 1} is 4 to 1 backwards
{1, 2, 4, 8, 16, 32, ...} is an infinite sequence where every term doubles
{a, b, c, d, e} is the sequence of the first 5 letters alphabetically
{f, r, e, d} is the sequence of letters in the name "fred"
{0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s (yes they are in order, it is an alternating order in this case)
Series
A series is the indicated sum of the terms of the sequence. A series can be donated by Sn, where in n refers to the number of terms. If a sequence is finite, its corresponding series is a finite series.
Example of series
* 2,4,6,8...S8
=S8= 2+4+6+8+10+12+14+16=72
2. Arithmetic Sequence
An arithmetic Sequence is a sequence in which the difference between any two consecutive terms is the same. This constant difference is called the common difference. and will be denoted by d.
To find any term
of an arithmetic sequence: where a1 is the first term of the sequence, d is the common difference, n is the number of the term to find. |
Examples
| Arithmetic Sequence | Common Difference, d | |
| 1, 4, 7, 10, 13, 16, ... |
d = 3
| add 3 to each term to arrive at the next term, or...the difference a2 - a1 is 3. |
| 15, 10, 5, 0, -5, -10, ... | d = -5 | add -5 to each term to arrive at the next term, or...the difference a2 - a1 is -5. |
| add -1/2 to each term to arrive at the next term, or....the difference a2 - a1 is -1/2. | ||
Examples
| Question | Answer |
| 1. Find the common difference for this arithmetic sequence 5, 9, 13, 17 ... | 1. The common difference, d, can be found by subtracting the first term from the second term, which in this problem yields 4. Checking shows that 4 is the difference between all of the entries. |
| 2. Find the common difference for the arithmetic sequence whose formula is an = 6n + 3 | 2. The formula indicates that 6 is the value being added (with increasing multiples) as the terms increase. A listing of the terms will also show what is happening in the sequence (start with n = 1). 9, 15, 21, 27, 33, ... The list shows the common difference to be 6. |
| 3. Find the 10th term of the sequence 3, 5, 7, 9, ... | 3. n = 10; a1 = 3, d = 2 The tenth term is 21. |
| 4. Find a7 for an arithmetic sequence where a1 = 3x and d = -x. | 4. n = 7; a1 = 3x, d = -x |
3. Arithmetic Series
An expression denoting the sum of the terms of an arithmetic sequence is called Arithmetic Series. An arithmetic series is finite if it is corresponding sequence is finite
Arithmetic Series
A series such as 3 + 7 + 11 + 15 + ··· + 99 or 10 + 20 + 30 + ··· + 1000 which has a constant didderencebetween terms. The first term is a1, the common difference is d, and the number of terms is n. The sum of an arithmetic series is found by multiplying the number of terms times the average of the first and last terms.
| Formula: | |
| Example: | 3 + 7 + 11 + 15 + ··· + 99 has a1 = 3 and d = 4. To find n, use theexplicit formula for an arithmetic sequence. We solve 3 + (n – 1)·4 = 99 to get n = 25. or |
A video about Arithmetic Series
Example of Arithmetic Series
a1=-3, d= 7, n=20
4. Geometric Sequence
If arithmetic sequence are formed by addition, Geometric Sequence are formed by multiplication each term in a geometric sequence is found by multiplying the previous term by the same number.A sequence with a common ratio is a Geometric Sequence.The constant multiplier in a geometric sequence is called a Common Ratio.
A geometric sequence with a definite number of terms is referred to as a finite geometric sequence.While a geometric sequence with indefinite number of terms is described as infinite geometric sequence.
If a sequence of values follows a pattern of multiplying a fixed amount (not zero) times each term to arrive at the following term, it is referred to as a geometric sequence. The number multiplied each time is constant (always the same).
The fixed amount multiplied is called the common ratio, r, referring to the fact that the ratio (fraction) of the second term to the first term yields this common multiple. To find the common ratio, divide the second term by the first term.
Examples:
| Geometric Sequence | Common Ratio, r | |
| 5, 10, 20, 40, ... |
r = 2
| multiply each term by 2 to arrive at the next term or...divide a2 by a1 to find the common ratio, 2. |
| -11, 22, -44, 88, ... | r = -2 | multiply each term by -2 to arrive at the next term .or...divide a2 by a1 to find the common ratio, -2. |
| multiply each term by 2/3 to arrive at the next term or...divide a2 by a1 to find the common ratio, 2/3. | ||
To find any term
of a geometric sequence:

where a1 is the first term of the sequence,
r is the common ratio, n is the number of the term to find.
of a geometric sequence:
where a1 is the first term of the sequence,
r is the common ratio, n is the number of the term to find.
Examples:
| Question | Answer |
| 1. Find the common ratio for the sequence | 1. The common ratio, r, can be found by dividing the second term by the first term, which in this problem yields -1/2. Checking shows that multiplying each entry by -1/2 yields the next entry. |
| 2. Find the common ratio for the sequence given by the formula | 2. The formula indicates that 3 is the common ratio by its position in the formula. A listing of the terms will also show what is happening in the sequence (start with n = 1). 5, 15, 45, 135, ... The list also shows the common ratio to be 3. |
| 3. Find the 7th term of the sequence 2, 6, 18, 54, ... | 3. n = 7; a1 = 2, r = 3 The seventh term is 1458. |
| 4. Find the 11th term of the sequence | 4. n = 11; a1 = 1, r = -1/2 |
| 5. Find a8 for the sequence 0.5, 3.5, 24.5, 171.5, ... | 5. n = 8; a1 = 0.5, r = 7 |
5. Geometric Series
The indicated sum of a geometric sequence is called a Geometric Series.
Finite Geometric Series
Finite Geometric Series
To find the sum of a finite geometric series, use the formula,
,
where is the number of terms, is the first term and is the common ratio.
,
where is the number of terms, is the first term and is the common ratio.
Example :
Find the sum of the first terms of the geometric series if and .
Example :
Find , the tenth partial sum of the infinite geometric series.
First, find .
Now, find the sum:
Infinite Geometric Series
An infinite geometric Series is the indicated sum of an infinite geometric sequence.
An infinite geometric series is the sum of an infinite geometric sequence. This series would have no last term. The general form of the infinite geometric series is , where is the first term and is the common ratio.
Infinite Geometric Series
To find the sum of an infinite geometric series having ratios with an absolute value less than one, use the formula, ,
where is the first term and is the common ratio.
Example :
Find the sum of the infinite geometric series
.
First find :
Then find the sum:
Example :
Find the sum of the infinite geometric series
if it exists.
First find :
Since is not less than one, the series does not converge. That is, it has no sum.
where is the first term and is the common ratio.
Example :
Find the sum of the infinite geometric series
.
.
First find :
Then find the sum:
Example :
Find the sum of the infinite geometric series
if it exists.
if it exists.
First find :
Since is not less than one, the series does not converge. That is, it has no sum.
6. Harmonic Sequence
A harmonic sequence is a special type of sequence in which the reciprocal of each terms forrs an arithmetic sequence
Given: 1, ½, 1/3, ¼…
Observe the denominators of each term in the sequence. Try to get the reciprocals. Do these form a sequence? If so, what type of sequence?
A sequence whose reciprocals form an arithmetic sequence is called a harmonic sequence.
find the a10 of the given example above.
Short video about Harmonic Sequence
7. Fibonacci Sequence
The Fibonacci Sequence is the series of numbers:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
The next number is found by adding up the two numbers before it.
- The 2 is found by adding the two numbers before it (1+1)
- Similarly, the 3 is found by adding the two numbers before it (1+2),
- And the 5 is (2+3),
- and so on!
It is that simple!
Here is a longer list:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...
Can you figure out the next few numbers?
Makes A Spiral
When we make squares with those widths, we get a nice spiral:
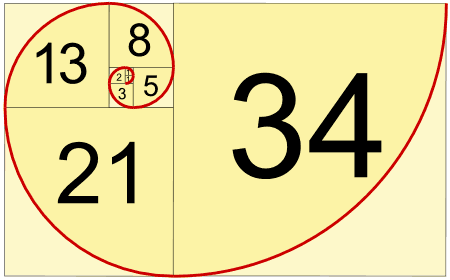
Do you see how the squares fit neatly together?
For example 5 and 8 make 13, 8 and 13 make 21, and so on.
For example 5 and 8 make 13, 8 and 13 make 21, and so on.
The Rule
The Fibonacci Sequence can be written as a "Rule" (see Sequences and Series).
First, the terms are numbered from 0 onwards like this:
| n = | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | ... |
| xn = | 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 | 377 | ... |
So term number 6 is called x6 (which equals 8).
Example: the 8th term is
the 7th term plus the 6th term: x8 = x7 + x6 | 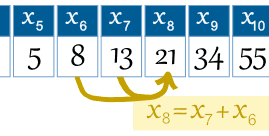 |
So we can write the rule:
The Rule is Fn = Fn-1 + Fn-2
where:
- Fn is term number "n"
- Fn-1 is the previous term (n-1)
- Fn-2 is the term before that (n-2)
Fibonacci Images
... Part 2
Sequence-is
a succession of set of number.
Series-is a
summation of all terms in a sequence.
Pattern-is
a set of number
a1
a2 a3 a4
1st 2nd 3rd 4th
1 ,
2 , 3 ,4...
a8 = ?
2 ,
4 ,6 ,8... =256
2 ,
4 ,8 ,16...
n = 8
5 ,
3 ,-1 ,-13...
Find the 9th
and S9 of the pattern.
1)
0.25,0.5,1...
Answer: 9th term = 64
S9 = 127.75
2)
0.25,0.5,0.75
Answer: 9th
term = 2.25
S9
=11.25
3)
4,1,-2...
Answer: 9th term = -20
S9
=-72
Arithmetic
Sequence
1 , 4,
7, 10, 13
10, 6, 2,
-2, 6
3
3 3 3 -4 -4
-4 -4
a1 a2
a3 a4 a5
1 4
7 10
13
1 1+3
1+2(3) 1+3(3) 1+4(3)
d =3
a1 a2
a3 a4 a5
10 6
2 -2 -6
10 10+(-4)
10+2(-4) 10+3(-4) 10+4(-4)
d =-4
Formula:
Nth term= a1+ (n-1) d
a1= 1st term
n= no. Of term
d= difference
a1=2 = 2+ (73) 5 SOLUTION
n=73 =2+360
2.) Find the 200term of the arithmetic
sequence of 3,5,7...
Answer: Nth term= a1+ (n-1) d
a200= 3+(200-1) 2
= 3+(199) 2
= 3+398
a200= 401
3.) Find the 350th term of
the arithmetic sequence if th first term is -13 and d=8.
Answer: Nth term= a1+ (n-1) d
a350= -13+(350-1) 8
= -13+(349) 8
= -13+2,792
a200= 2,779
Activity:
1) a1=7,d=4, a100=?
an= a1+ (n-1) d
a350= 7+(100-1)4
= 7+(99) 4
= 7+394
a200= 403
2)
a1=?,
a150=353, d=3 3) d=?, a1=11, a120= 130
an=
a1+ (n-1) d an= a1+
(n-1) d
353= a1+(150-1)3 130= 11+(120-1)d
353= a1+(149) 3 130= 11+119 d
353= a1+447 130-11=119 d
353-447=a1 119 = 119d
a1= -94 119 119
d=1
Arithmetic
Series
Carl
Friedrich Gauss
1,2,3,4........97,98,99,100
=5,050
Formula:
Sn=(a1+an)(n/2)
=[a1+a1+(n-1)](n/2)
=[2a1+(n-1)d](n/2)] formula of Arithmetic
Series
Ex.
1)
Find
the sum of all integers that are multiples of four fom 1-150.
Answer:
a1=4 an=148 d=4
n=37
[2a1+(n-1)d](n/2)]
[2(4)+(37-1)4](n/2)
[8+ 36(4)(37/2)]
[8+144)(37/2)]
152(18.5)
Sn= 2,812
2)
Find
the sum of all positive integers of 30-500 that are multiples of 6.
Answer:
a1=30 an=498 d=6
n=83
[2a1+(n-1)d](n/2)]
[2(30)+(83-1)6](83/2)
[60+492)(83/2)
552(41.5)
Sn= 22,908
3)
Find
the sum of all positive integers of 20-1000 that are divisible by 7.
Answer:
a1=21 an=994 d=7
n=142
[2a1+(n-1)d](n/2)]
[2(21)+(142-1)7](42/2)
[42+ 141(7)(71)]
42+987(71)
1029(71)
Sn= 73,059
Geometric
Sequence- a sequence that has a common ratio(r).
Common Ratio
The constant factor between consecutive terms of a geometric sequence is called the common ratio.
Example:
Given the geometric sequence .
To find the common ratio, find the ratio between a term and the term preceding it.
is the common ratio.
r=2
Formula
of ratio: an
or r= a2
an-1
a1
Geometric
Sequence
Formula: an=a1(r)n-1
Ex: 1)
a1=2 r=-x a10=?
Answer: an=a1(r) n-1
=-2(-x)9
=2(-x9)
a10=-2x9
2)a1=x r=y
Answer: an=a1(r) n-1
=x(y)9
=x(y9)
a10=xy9
3)a1=5
r=-2
Answer: an=a1(r) n-1
=5(-2)9
=5(-512)
a10=-2560
Geometric
Series
(Finite Geometric Series)
Formula:
Sn= a1 (rn-1)
r-1
Ex: 1) a1=x, r=2 S20=?
Answer:
Sn= a1 (rn-1)
r-1
=x (2 20 -1)
2-1
=x
(1,048,575)
1
S20 = 1,048575x
2) a1=2/y ,r=3, S12=?
Answer: Sn= a1 (rn-1)
r-1
=2/y (3 12 -1)
3-1
=2/y(531,440)
2
=2/y(265,720)
S12 = 531,440
y
3)a1=17
r=-1 ,S29=?
Answer:
Sn= a1 (rn-1)
r-1
=17 (-1 29 -1)
-1-1
=17(-2)
-2
= -34
-2
Sn=17
Geometric
Series
(Infinite Geometric Series)
Formula:
Sn= a1
1-r
Ex: 1) 100,50,25
Answer:
r=1/2
Sn= a1
1-r
=
1-1/2
= 100
½
= 100(2)
Sn = 200
2)2,6,13...
r=3
not exist
Remember: If the ratio is greater than 1it is
not exist.
3)1000,100,10...
Answer: r=1/2
Sn= a1
1-r
= 1000
1-1/10
= 1000
9/10
= 1000(10/9)
Sn = 10,000
9
Harmonic
Sequence
Formula: an= 1
a1+(n-1)d
Ex: 1) a1=1/3, d=4, a50=?
Answer:
an= 1
a1+(n-1)d
=
1
3+(50-1)4
=
1
199
2) 3/5, 1/3, 3/13...a35=?
Answer:
d=4 n=75
an= 3
a1+(n-1)d
=
3
5+(75-1)4
=5+(74)4
=
3
301
3) 2/5, 1/5, 2/15...a100=?
Answer:
d=5 n=100
an= 2
a1+(n-1)d
=
2
5+(100-1)5
=5+(99)5
=
2
500
= 1
250