...Part 1

1. Patterns

• set of number or sequence.
• Repeated design or recurring sequence.
• An ordered set of numbers, shapes or other mathematical objects, arranged according to a rule.

Try to get the pattern of this picture

Short video about Math Patterns...

Sequence

A Sequence is a succession of numbers in a specific order.Each number in a sequence is called terms. The terms are formed according to some fixed rule or property. They are arranged as the first term, the second term, the third term and so on. A sequence with a definite number of term is a finite sequence.

                           

Examples:

{1, 2, 3, 4, ...} is a very simple sequence (and it is an infinite sequence)

{20, 25, 30, 35, ...} is also an infinite sequence

{1, 3, 5, 7} is the sequence of the first 4 odd numbers (and is a finite sequence)

{4, 3, 2, 1} is 4 to 1 backwards

{1, 2, 4, 8, 16, 32, ...} is an infinite sequence where every term doubles

{a, b, c, d, e} is the sequence of the first 5 letters alphabetically

{f, r, e, d} is the sequence of letters in the name "fred"

{0, 1, 0, 1, 0, 1, ...} is the sequence of alternating 0s and 1s (yes they are in order, it is an alternating order in this case)

Series

A series is the indicated sum of the terms of the sequence. A series can be donated by Sn, where in n refers to the number of terms. If a sequence is finite, its corresponding series is a finite series.

Example of series

* 2,4,6,8...S8

=S8= 2+4+6+8+10+12+14+16=72

2. Arithmetic Sequence

An arithmetic Sequence is a sequence in which the difference between any two consecutive terms is the same. This constant difference is called the common difference. and will be denoted by d.

To find any term  of an arithmetic sequence: where a1 is the first term of the sequence, d is the common difference, n is the number of the term to find.

Examples

Arithmetic Sequence	Common Difference, d
1, 4, 7, 10, 13, 16, ...	d = 3	add 3 to each term to arrive at the next term, or...the difference  a2 - a1 is 3.
15, 10, 5, 0, -5, -10, ...	d = -5	add -5 to each term to arrive at the next term, or...the difference  a2 - a1 is -5.
		add -1/2 to each term to arrive at the next term, or....the difference a2 - a1 is -1/2.

Examples

Question	Answer
1.  Find the common difference for this arithmetic sequence                           5, 9, 13, 17 ...	1.  The common difference, d, can be found by subtracting the first term from the second term, which in this problem yields 4.  Checking shows that 4 is the difference between all of the entries.
2.  Find the common difference for the arithmetic sequence whose formula is                          an = 6n + 3	2. The formula indicates that 6 is the value being added (with increasing multiples) as the terms increase.  A listing of the terms will also show what is happening in the sequence (start with n = 1).                            9, 15, 21, 27, 33, ... The list shows the common difference to be 6.
3.  Find the 10th term of the sequence                           3, 5, 7, 9, ...	3. n = 10;  a1 = 3, d = 2  The tenth term is 21.
4.  Find a7 for an arithmetic sequence where                   a1 = 3x and d = -x.	4.  n = 7;  a1 = 3x, d = -x

3. Arithmetic Series

An expression denoting the sum of the terms of an arithmetic sequence is called Arithmetic Series. An arithmetic series is finite if it is corresponding sequence is finite

Arithmetic Series

A series such as 3 + 7 + 11 + 15 + ··· + 99 or 10 + 20 + 30 + ··· + 1000 which has a constant didderencebetween terms. The first term is a₁, the common difference is d, and the number of terms is n. The sum of an arithmetic series is found by multiplying the number of terms times the average of the first and last terms.

Formula:
Example:	3 + 7 + 11 + 15 + ··· + 99 has a1 = 3 and d = 4. To find n, use theexplicit formula for an arithmetic sequence. We solve 3 + (n – 1)·4 = 99 to get n = 25. or

A video about Arithmetic Series

Example of Arithmetic Series

a1=-3, d= 7, n=20

4. Geometric Sequence

If arithmetic sequence are formed by addition, Geometric Sequence are formed by multiplication each term in a geometric sequence is found by multiplying the previous term by the same number.A sequence with a common ratio is a Geometric Sequence.The constant multiplier in a geometric sequence is called a Common Ratio.

A geometric sequence with a definite number of terms is referred to as a finite geometric sequence.While a geometric sequence with indefinite number of terms is described as infinite geometric sequence.

If a sequence of values follows a pattern of multiplying a fixed amount (not zero) times each term to arrive at the following term, it is referred to as a geometric sequence.   The number multiplied each time is constant (always the same).

     The fixed amount multiplied is called the common ratio, r, referring to the fact that the ratio (fraction) of the second term to the first term yields this common multiple.  To find the common ratio, divide the second term by the first term.

Examples:

Geometric Sequence	Common Ratio, r
5, 10, 20, 40, ...	r = 2	multiply each term by 2 to arrive at the next term or...divide a2 by a1 to find the common ratio, 2.
-11, 22, -44, 88, ...	r = -2	multiply each term by -2 to arrive at the next term .or...divide a2 by a1 to find the common ratio, -2.
		multiply each term by 2/3 to arrive at the next term or...divide a2 by a1 to find the common ratio, 2/3.

To find any term 
of a geometric sequence:

where a₁ is the first term of the sequence,
r is the common ratio, n is the number of the term to find.

Examples:

Question	Answer
1.  Find the common ratio for the sequence	1.  The common ratio, r, can be found by dividing the second term by the first term, which in this problem yields -1/2.  Checking shows that multiplying each entry by -1/2 yields the next entry.
2.  Find the common ratio for the sequence given by the formula	2.  The formula indicates that 3 is the common ratio by its position in the formula.  A listing of the terms will also show what is happening in the sequence (start with n = 1).                            5, 15, 45, 135, ... The list also shows the common ratio to be 3.
3.  Find the 7th term of the sequence                          2, 6, 18, 54, ...	3. n = 7;  a1 = 2, r = 3 The seventh term is 1458.
4.  Find the 11th term of the sequence	4.  n = 11;  a1 = 1, r = -1/2
5.  Find  a8 for the sequence                    0.5, 3.5, 24.5, 171.5, ...	5.  n = 8;  a1 = 0.5,  r = 7

5. Geometric Series

The indicated sum of a geometric sequence is called a Geometric Series.

Finite Geometric Series

Finite Geometric Series

To find the sum of a finite geometric series, use the formula,
Sn=a1(1−rn)1−r,r≠1$S_n=\frac{a_1\left(1-r^n\right)}{1-r},r\ne 1$,
where n$n$ is the number of terms, a1$a_1$ is the first term and r$r$ is the common ratio.

Example :

Find the sum of the first 8$8$ terms of the geometric series if a1=1$a_1=1$ and r=2$r=2$.

S8=1(1−28)1−2=255$S_8=\frac{1\left(1-2^8\right)}{1-2}=255$

Example :

Find S10$S_{10}$, the tenth partial sum of the infinite geometric series24+12+6+...$24+12+6+\mathrm{...}$.

First, find r$r$. 

r=a2a1=1224=12$r=\frac{a_2}{a_1}=\frac{12}{24}=\frac{1}{2}$

Now, find the sum:

S10=24(1−(12)10)1−12=306964

Infinite Geometric Series

An infinite geometric Series is the indicated sum of an infinite geometric sequence.

An infinite geometric series is the sum of an infinite geometric sequence. This series would have no last term. The general form of the infinite geometric series is a1+a1r+a1r2+a1r3+...$a_1+a_{1}r+a_1{r}^2+a_1{r}^3+\mathrm{...}$ , where a1$a_1$ is the first term and r$r$ is the common ratio.

Infinite Geometric Series

To find the sum of an infinite geometric series having ratios with an absolute value less than one, use the formula, S=a11−r$S=\frac{a_1}{1-r}$,
where a1$a_1$ is the first term and r$r$ is the common ratio.

Example :

Find the sum of the infinite geometric series
27+18+12+8+...$27+18+12+8+\mathrm{...}$.

First find r$r$: 

r=a2a1=1827=23$r=\frac{a_2}{a_1}=\frac{18}{27}=\frac{2}{3}$

Then find the sum:

S=a11−rS=271−23=81$\begin{array}{l}S=\frac{a_1}{1-r}\\ S=\frac{27}{1-\frac{2}{3}}=81\end{array}$

Example :

Find the sum of the infinite geometric series
8+12+18+27+...$8+12+18+27+\mathrm{...}$ if it exists.

First find r$r$:

r=a2a1=128=32$r=\frac{a_2}{a_1}=\frac{12}{8}=\frac{3}{2}$

Since r=32$r=\frac{3}{2}$ is not less than one, the series does not converge. That is, it has no sum.

6. Harmonic Sequence

A harmonic sequence is a special type of sequence in which the reciprocal of each terms forrs an arithmetic sequence

Given: 1, ½, 1/3, ¼…

  Observe the denominators of each term in the sequence. Try to get the reciprocals. Do these form a sequence? If so, what type of sequence?

            A sequence whose reciprocals form an arithmetic sequence is called a harmonic sequence.

find the a10 of the given example above.

Short video about Harmonic Sequence

7. Fibonacci Sequence

The Fibonacci Sequence is the series of numbers:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...

The next number is found by adding up the two numbers before it.

• The 2 is found by adding the two numbers before it (1+1)
• Similarly, the 3 is found by adding the two numbers before it (1+2),
• And the 5 is (2+3),
• and so on!

Example: the next number in the sequence above is 21+34 = 55

It is that simple!

Here is a longer list:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, ...

Can you figure out the next few numbers?

Makes A Spiral

When we make squares with those widths, we get a nice spiral:

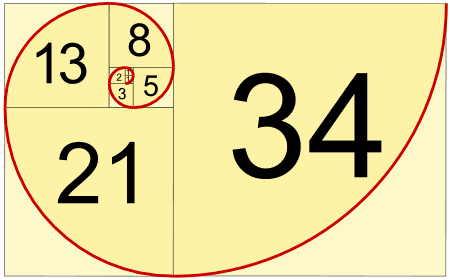
Do you see how the squares fit neatly together?
For example 5 and 8 make 13, 8 and 13 make 21, and so on.

The Rule

The Fibonacci Sequence can be written as a "Rule" (see Sequences and Series).

First, the terms are numbered from 0 onwards like this:

n =	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	...
xn =	0	1	1	2	3	5	8	13	21	34	55	89	144	233	377	...

So term number 6 is called x₆ (which equals 8).

Example: the 8th term is the 7th term plus the 6th term: x8 = x7 + x6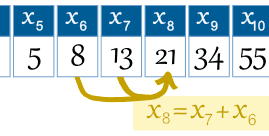

So we can write the rule:

The Rule is F_n = F_n-1 + F_n-2

where:

• _Fn is term number "n"
• _Fn-1 is the previous term (n-1)
• _Fn-2 is the term before that (n-2)

Example: term 9 is calculated like this:

F9	= F9-1 + F9-2
	= F8 + F7
	= 21 + 13
	= 34

 Fibonacci Images

... Part 2

Sequence-is a succession of set of number.

Series-is a summation of all terms in a sequence.

Pattern-is a set of number

a1  a2  a3  a4

1^st  2^nd  3^rd  4^th

1 ,  2  , 3  ,4...         a8 = ?

2 ,  4  ,6  ,8...            =256

2 ,  4  ,8  ,16...         n = 8

5 ,  3  ,-1  ,-13...

Find the 9^th and S9 of the pattern.

1)        0.25,0.5,1...

Answer:  9^th term = 64

            S9 = 127.75

2)        0.25,0.5,0.75

Answer: 9^th term = 2.25

          S9  =11.25

3)        4,1,-2...

 Answer: 9^th term = -20

           S9  =-72

Arithmetic Sequence- a sequence with a common difference.

Arithmetic Sequence

   1 , 4,  7,  10,  13             10,  6,  2,  -2,  6

 

                               

     3  3   3   3                 -4  -4  -4   -4

a1    a2   a3      a4      a5

1     4    7       10     13 

1    1+3  1+2(3)  1+3(3)  1+4(3)   

   

        d =3

d/difference

a1    a2       a3        a4         a5

10    6        2         -2        -6 

10    10+(-4)  10+2(-4)  10+3(-4)   10+4(-4)   

   

        d =-4

Formula:

        Nth term= a1+ (n-1) d

    

      a1= 1^st term

       n= no. Of term

       d= difference

    Ex: 1.)  2,7,12...              GIVEN   

                                Nth term= a1+ (n-1) d         FORMULA

               a73  d=5             a73= 2+(200-1) 5

                    a1=2               = 2+ (73) 5          SOLUTION

                    n=73               =2+360

                                    a73=363              ANSWER

      

       2.) Find the 200term of the arithmetic sequence of 3,5,7...

            

         Answer:  Nth term= a1+ (n-1) d

                  a200= 3+(200-1) 2

                      = 3+(199) 2

                      = 3+398

                  a200= 401

       3.) Find the 350^th term of the arithmetic sequence if th first term is -13 and d=8.

       

          Answer:  Nth term= a1+ (n-1) d

                  a350= -13+(350-1) 8

                      = -13+(349) 8

                      = -13+2,792

                  a200= 2,779

Activity:

1)    a1=7,d=4, a100=?    

  

       an= a1+ (n-1) d

         a350= 7+(100-1)4

             = 7+(99) 4

             = 7+394

         a200= 403

2)        a1=?, a150=353, d=3              3)  d=?, a1=11, a120= 130

     an= a1+ (n-1) d                   an= a1+ (n-1) d      

         353= a1+(150-1)3                 130= 11+(120-1)d

         353= a1+(149) 3                  130= 11+119 d

         353= a1+447                     130-11=119 d

         353-447=a1                        119  = 119d

          a1= -94                           119   119

                                              d=1

Arithmetic Series

Carl Friedrich Gauss

      1,2,3,4........97,98,99,100

           =5,050

Formula:

        Sn=(a1+an)(n/2)

          =[a1+a1+(n-1)](n/2)

          =[2a1+(n-1)d](n/2)] formula of Arithmetic Series

               

Ex. 

1)        Find the sum of all integers that are multiples of four fom 1-150.

 Answer:     a1=4  an=148  d=4  n=37

               [2a1+(n-1)d](n/2)]

               [2(4)+(37-1)4](n/2)

               [8+ 36(4)(37/2)]

               [8+144)(37/2)]

                 152(18.5)

            Sn= 2,812

2)        Find the sum of all positive integers of 30-500 that are multiples of 6.

  Answer:     a1=30  an=498  d=6  n=83

               [2a1+(n-1)d](n/2)]

               [2(30)+(83-1)6](83/2)

               [60+492)(83/2)

                 552(41.5)

            Sn= 22,908

3)        Find the sum of all positive integers of 20-1000 that are divisible by 7.

  Answer:    a1=21  an=994  d=7  n=142

              [2a1+(n-1)d](n/2)]

               [2(21)+(142-1)7](42/2)

               [42+ 141(7)(71)]

                42+987(71)

                 1029(71)

            Sn= 73,059

     

Geometric Sequence- a sequence that has a common ratio(r).

Common Ratio

The constant factor between consecutive terms of a geometric sequence is called the common ratio.

Example:

Given the geometric sequence 2,4,8,16,...$2,4,8,16,\mathrm{...}$.

To find the common ratio, find the ratio between a term and the term preceding it. 

r=42=2$r=\frac{4}{2}=2$

2$2$ is the common ratio.

       

          r=2

Formula of ratio:  an   or  r= a2

               an-1        a1

  

Geometric Sequence

   

 Formula: an=a1(r)n-1

Ex:    1)    a1=2  r=-x  a10=?

       

         Answer:   an=a1(r) n-1

                     =-2(-x)9

                     =2(-x9)

                  a10=-2x9

    

      2)a1=x  r=y

        Answer:   an=a1(r) n-1

                     =x(y)9

                     =x(y9)

                  a10=xy9

    

      3)a1=5  r=-2

         Answer:   an=a1(r) n-1

                     =5(-2)9

                     =5(-512)

                  a10=-2560

Geometric Series

   (Finite Geometric Series)

 

Formula:    Sn= a1 (rn-1)

                   r-1

Ex:  1) a1=x, r=2 S20=?

     

     Answer:   Sn= a1 (rn-1)

                    r-1

                =x (2 20 -1)

                     2-1

                =x (1,048,575)

                      1

              S20 = 1,048575x

    2) a1=2/y ,r=3, S12=?

        

        Answer:   Sn= a1 (rn-1)

                       r-1

                   =2/y (3 12 -1)

                        3-1

                   =2/y(531,440)

                         2

                   =2/y(265,720)

                 S12 = 531,440

                        y              

   3)a1=17  r=-1 ,S29=?

       Answer:   Sn= a1 (rn-1)

                       r-1

                   =17 (-1 29 -1)

                        -1-1

                   =17(-2)

                       -2

                    = -34

                      -2 

                Sn=17

           

Geometric Series

   (Infinite Geometric Series)

Formula:  Sn= a1

             1-r

Ex:  1) 100,50,25

        

 Answer:   r=1/2

       

         Sn= a1

            1-r

           == 100

             1-1/2

          

           = 100

             ½

             

           = 100(2)

         Sn = 200

2)2,6,13...

   r=3

  not exist

Remember: If the ratio is greater than 1it is not exist.

3)1000,100,10...

Answer:   r=1/2

       

         Sn= a1

            1-r

           = 1000

             1-1/10

          

           = 1000

             9/10

             

           = 1000(10/9)

        

        Sn = 10,000

              9             

Harmonic Sequence

 Formula:   an=    1  

                      a1+(n-1)d

Ex:  1) a1=1/3, d=4, a50=?

   Answer:       an=    1  

                           a1+(n-1)d

                  =    1   

                    3+(50-1)4

                  =    1 

                      199    

      2) 3/5, 1/3, 3/13...a35=?

    

    Answer:      

              d=4   n=75

                an=    3  

                     a1+(n-1)d

                  =    3   

                    5+(75-1)4

                  =5+(74)4

                  =    3 

                      301    

     

      3) 2/5, 1/5, 2/15...a100=?

        Answer:      

              d=5   n=100

                an=    2  

                     a1+(n-1)d

                  =    2   

                    5+(100-1)5

                  =5+(99)5

                  =    2 

                      500 

                  =    1  

                      250